The Five Minute Guide to Complex Numbers

Real Numbers

Real numbers are the numbers that we use every day: 1, 2, 3, π, √2, etc. They lie along a horizontal line running from -∞ to ∞.

Imaginary Numbers

The square root of 4 is 2 because 2 × 2 is 4. However, -2 × -2 is also 4 so we can note that 4 has two square roots and 2 is the principal square root of 4. Furthermore, we can state that every real number has two distinct square roots (apart from 0 which has two indistinct square roots, 0 and -0). This leads to a question: if -2 isn't the square root of -4, what is?

Before we answer that, let's ask: what is the square root of -1? To answer that question, we define a number that we call the imaginary unit, denoted by i, such that i × i = -1. Now we can answer the question about the square root of -4:

√-4 = ±2i

i and 2i are imaginary numbers. Imaginary numbers lie along a vertical line running from ∞ to -∞.

Despite the name, imaginary numbers are no less real than real numbers. Or more real for that matter. Real numbers are a useful abstraction of physical quantities but that doesn't mean that physical quantities behave the same as real numbers. For example, real numbers are infinitely divisible, but an electric current of 1A isn't: electric current and charge come in integer multiples of a fundamental physical quantity, the charge of an electron. So just think of imaginary numbers as numbers.

Complex Numbers

Complex numbers have both a real part and an imaginary part. Unlike real numbers and imaginary numbers that lie on lines, complex numbers form a plane. We write complex numbers as the real part followed by the imaginary part, remembering to include the sign of the imaginary part:

3+4i
1-2i
-0.01+0.02i

This form is called the rectangular form. Complex numbers can be represented in another way called polar form which we'll cover shortly. In mathematics, it is conventional to represent an unknown real quantity using the letter x. An unknown complex number is represented by the letter z,

You may also see j used to denote the imaginary unit; this is a convention in various engineering disciplines where I represents an electric current and avoids confusion. It's the same thing.

Complex Arithmetic

Addition and Subtraction

To add and subtract complex numbers, we simply add / subtract the real and imaginary components separately:

x+yi + a+bi = (x + a) + (y + b)i
x+yi - a+bi = (x - a) + (y - b)i
1+3i + 4-2i = 5+i
1+3i - 4-2i = -3+5i

Multiplication

To multiply complex numbers we need to multiply the components of each number by each other:

x+yi × a+bi = (xa - yb) + (xb + ya)i
1+3i × 4-2i = (4+6) + (12-2)i = 10+10i

The '-' sign in the real component of the product is because the product of two imaginary numbers is real and, by definition, i2 is -1.

Squaring

The square of a complex number is the expansion of (x+yi)2:

(x+yi)2 = (x2 - y2) + 2xyi
(1+3i)2 = -8+6i

Complex Conjugate

The conjugate of a complex number, written z*, is the same number but with the imaginary sign reversed:

(1+3i)* = 1-3i

Multiplying a complex number by its conjugate has the useful property of cancelling out the imaginary part leaving just a real number:

x+yi × x-yi = x2 + y2
1+3i × 1-3i = 10

Division

We can't divide complex numbers directly. What we can do is multiply the top and bottom by some number. If that number just so happens to be the complex conjugate of the denominator, we end up with an easy division:

(x+yi) / (a+bi) = (x+yi)(a-bi) / (a2 + b2)
(1+2i) / (2-i) = (1+2i)(2+i) / 5 = 5i / 5 = i

Reciprocal

We can use the division formula to calculate the reciprocal of a complex number:

(x+yi)-1 = (x-yi) / (x2 + y2)
(1+3i)-1 = (1-3i) / 10 = 0.1-0.3i

Modulus

The modulus of a complex number, denoted by |z| is the length of the line from 0 to the point in the complex plane. We calculate it using Pythagoras' Theorem:

|x+yi| = √(x2+y2)
|3-4i| = 5

Polar Form

If we draw a point on the complex plane, an alternate representation presents itself:

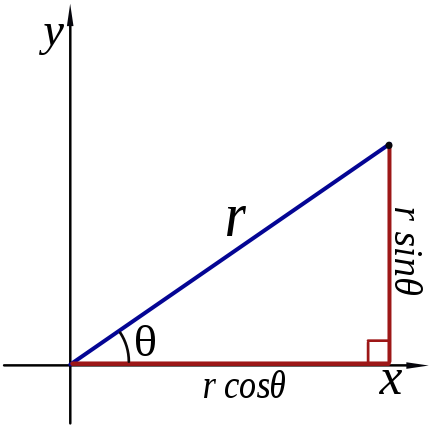
A point in the complex plane (credit: Wikimedia Commons)

r is the modulus of x+yi. The value of 𝜃 can be obtained using basic trigonometry: y/x is the tangent of 𝜃 so 𝜃 is the arctangent of y/x. If you're a programmer, any maths library will provide a two argument arctangent method, typically called atan2. You can try it out yourself: to calculate the angle of 3-4i, bring up the browser console and typeMath.atan2(-4,3) (note that the value is in radians and will be negative when the value of y is negative).

Once we have obtained r and 𝜃, we write the number in polar form, like this: 

r cis 𝜃

cis stands for "cosine plus i sine". The diagram shows how to convert back to rectangular form:

r cis 𝜃 → r(cos 𝜃 + i sin 𝜃)

So why should we go to all this trouble? The reason is that it makes various calculations significantly easier:

Multiplication: (r cis 𝜃)(s cis φ) = rs cis (𝜃 + φ)
Division:       (r cis 𝜃) / (s cis φ) = r/s cis (𝜃 - φ)
Exponentiation: (r cis 𝜃)n = rn cis n𝜃

Also, if we visualize all numbers as a vector with a magnitude and bearing even the arithmetic that we're used to suddenly makes a lot more sense. Why does multiplying two negatives make a positive? And then multiplying by a negative again flip the sign back? If we think about adding angles, then multiplying by a negative number is an addition of 180°. Because of the nature of a circle, 180° + 180° is equivalent to 0°, resulting in a positive number. Add 180° again and we're back to negative. The numbers aren't flipping at all - they're rotating around a circle. Why do all numbers have two square roots? Because squaring involves a doubling of the angle. Numbers separated by 180° will end up at the same place on the circle when their angles are doubled. So 1 cis 90° (i) will square to 1 cis 180° (-1). 1 cis 270° (-i) will square to 1 cis 540° which is equivalent to 1 cis 180° (-1 again). So rather than making arithmetic more obscure, complex numbers actually demystify it. And they promote imaginary numbers from their lowly position as "the square roots of negative numbers".

Unfortunately, we cannot do addition and subtraction in polar form so need to convert back to rectangular form to do those operations.

There you go: that's all the complex arithmetic required to understand the fractal formulae used in the application.

Back to the index