Variations on the Mandelbrot Set Formula
The Phoenix Fractal
The Phoenix fractal formula takes the quadratic formula and adds feedback from the previous values of the iteration:
zk+1 = zk2 + c + P·zk-1
P is an additional complex parameter to the iteration. If it is equal to 0, we have the standard quadratic iteration function. The initial values are:
z0 = im(z)+re(z)i, z-1 = 0
The initialization of z0 swaps the real and imaginary components of z to present a side-by-side view of the fractal rather than top-to-bottom. Exterior distance estimation also requires us to keep track of the previous value:
dz0 = 1, dz-1 = 0 dzk+1 = 2·dzk·zk + P·dzk-1
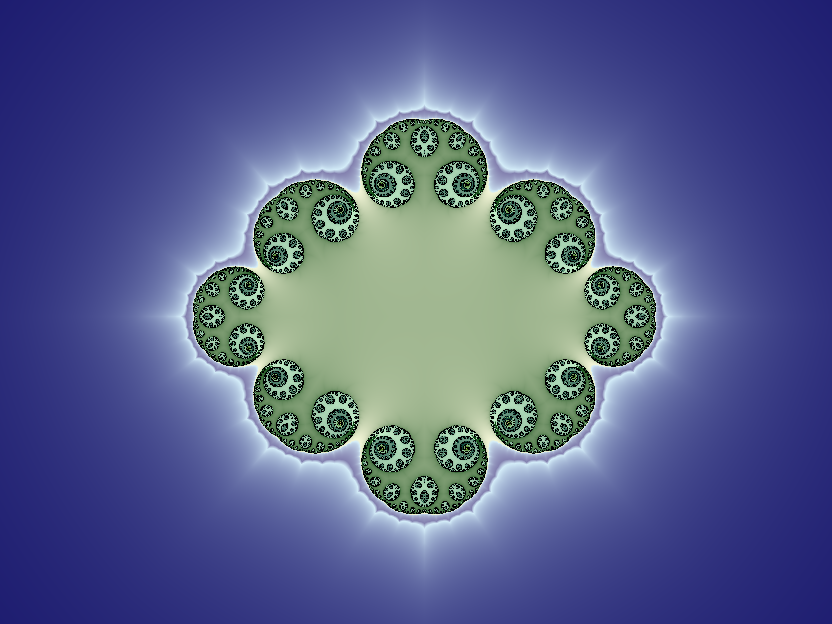
Here is the Phoenix fractal using Ushiki's parameters:
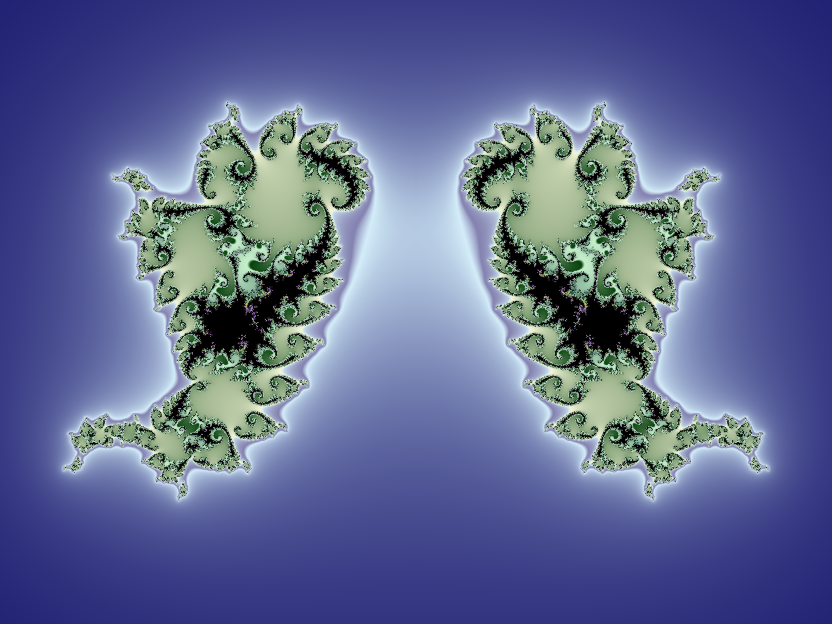
A variety of parameters around c≈0.55 and P≈-0.5 will produce Phoenixes:
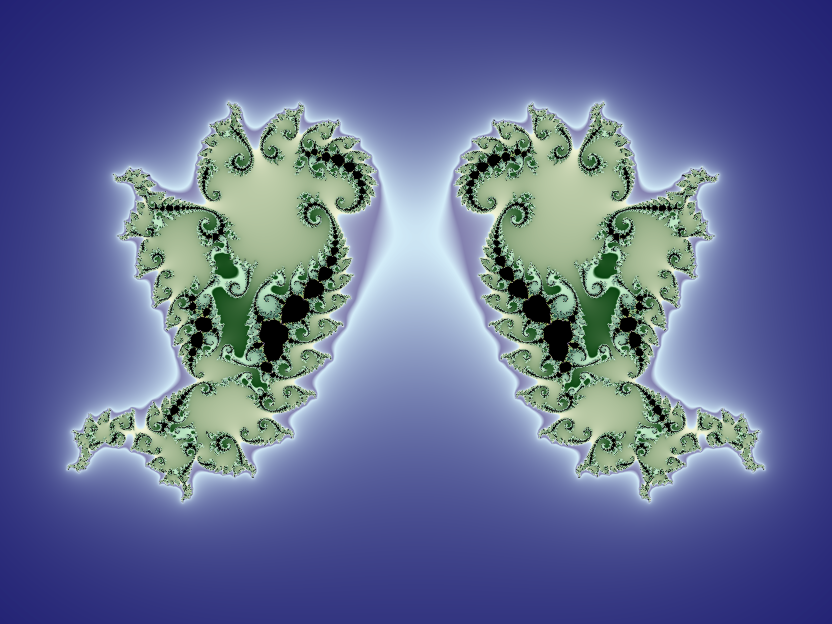
Adding a small amount of feedback to quadratic Julia sets can create attractive results:
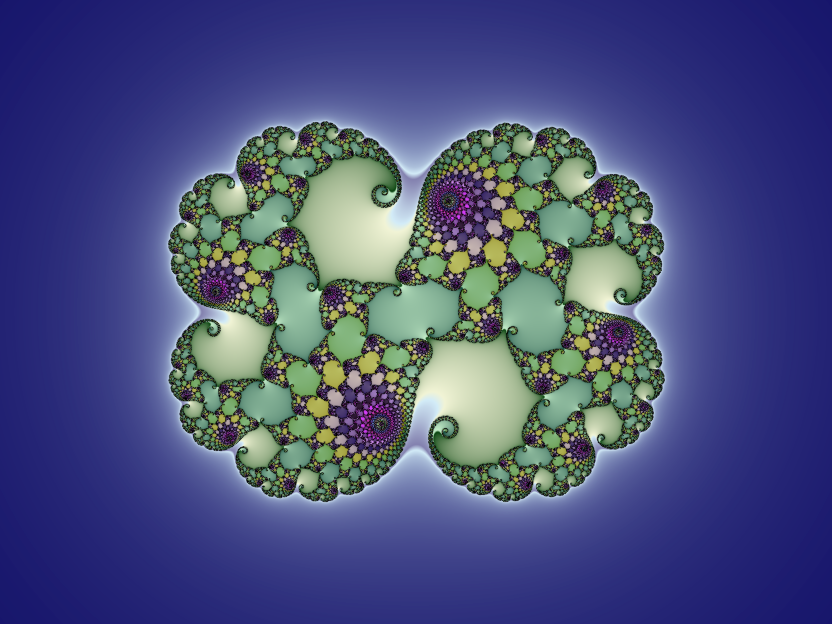
Otherwise, this is a tough fractal to work with. Any imaginary component in c will result in unattractive asymmetries. We don't even have a Julia map to help us out.
- The resulting images are extremely ugly
- The Mandelbrot sets are useless as maps to Julia sets
The Burning Ship Fractal
The Burning ship formula varies the quadratic formula by squaring the absolute value of zk:
zk+1 = (|re(zk)| + |im(zk)|i)2 - c
Note, we subtract c on each iteration so that the burning ship is rendered right side up. If I'm honest, the result isn't exactly pretty:

That said, there are some notable features worth exploring. The tail on the lower right is known as the armada and is really quite striking:

Disabling exterior colouring picks out the structure of the pylons:

Burning Ship Julia Sets
The Mandelbrot set is a fair Julia set map. Where the Burning Ship is messy, such as the superstructure, the Julia sets are also messy. There are three areas worth exploring, however.
If you click in the area close to the bow, you will see forms that put me in mind of dissected frogs, like this:

The perfect bilateral symmetry, despite the imaginary component of c, is characteristic of the formula. The Armada area produces interesting structures, although they look best without external colouring:

The strip underneath the keel closes to the hull produces quite beautiful images: