Mandelbrot and Julia Sets Using Other Powers of z
We can generalize the iteration function that produces the Mandelbrot set and the quadratic Julia sets to:
z → zP + c
Mandelbrot Sets for Powers of z >2
If simply squaring z each time produces such a variety of forms, images produced by higher powers of z should be simply amazing, right? See for yourself:





Compare these images to the quadratic Mandelbrot set, drawn to the same scale:

The Multibrot sets show P-1 rotational symmetry - you can rotate the z4 Mandelbrot set through 120° and obtain the same image. One geometric feature is apparent immediately. For a given power P, the Mandelbrot set has P-1 cusps. If we zoom into the bulbs sprouting from the central cardioids other features become apparent:



The bulbs also have cusps, P-2 of them, to be precise. There are also P-1 prominent antennae.
Comparing the P=2 image to the others, the standard Mandelbrot set has a "halo" that quickly disappears - it is pretty much gone by P=5. The halo is where all the interesting stuff is to be found. What's happening? The answer is to be found in the "+ c" component of the iteration function. Remember that we're dealing exclusively with small numbers: |z| <= 2. For P=2, c is significant. Without c, we would get a unit circle since small numbers would become smaller under iteration and larger numbers would just become larger. Adding a constant number each iteration mixes things up and produces all the marvellous chaos that makes the Mandelbrot set endlessly fascinating. As we increase P, c becomes less and less significant and the Mandelbrot set converges on the unit circle:





Look again at the bulb images. The "minibrots" that are a notable feature of the Mandelbrot set landscape become larger and dominate the landscape. The boundary becomes narrower, denser and less distinct. In conclusion: Mandelbrot sets for P>2 are less interesting.
Julia Sets for Powers of z >2
The quadratic Julia sets have 2-fold rotational symmetry (i.e., rotate the image through 180° and you have the same image). For P > 2, the Julia sets have P-fold rotation symmetry, which means, for higher P, P-pointed stars which can be very attractive indeed:




The Multibrot sets retain the property of being a useful directory for Julia sets:
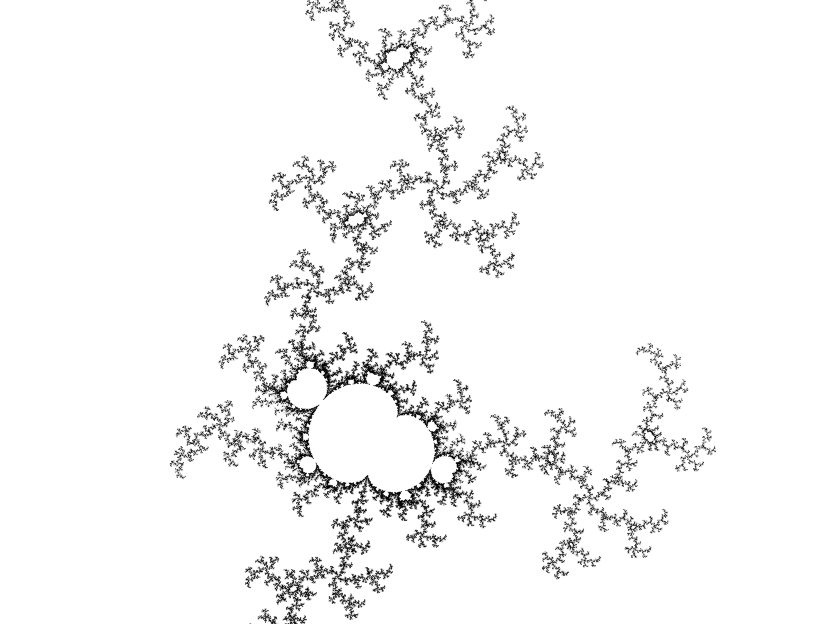
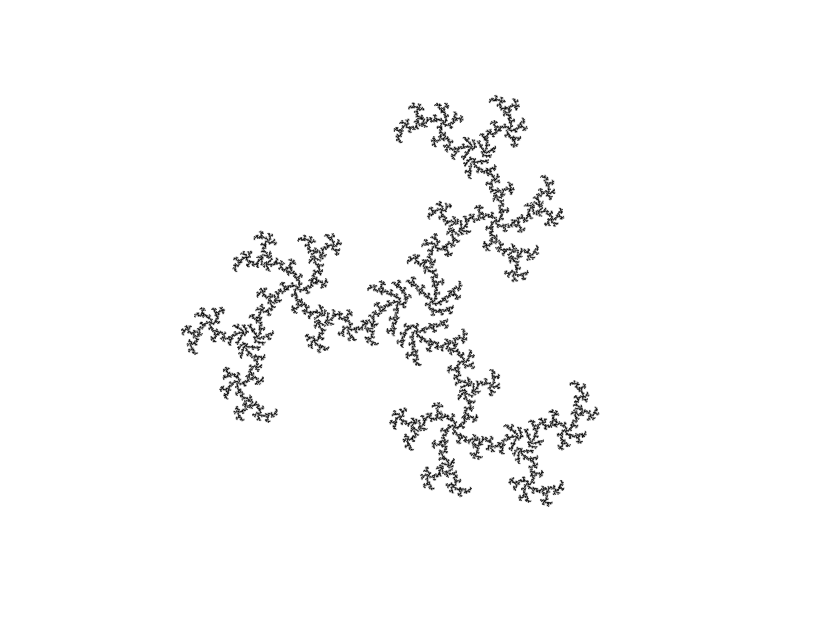
Mandelbrot Sets for Powers of z <=2
There is nothing to stop you from using a negative exponent. The results are striking:





Note that the default colouring options reverse the colours for the boundary and set "interior". The sets are no longer compact, but extend out to infinity. They encircle, but do not include, the origin. They have rotational symmetry of order |P| + 1. The large red discs are somewhat fishy: they are an artefact of the generation algorithm, specifically the choice of escape value. Reciprocal functions are "bouncy". Take a number, square it then take its reciprocal; most numbers become small. Square it again and take its reciprocal and the value bounces right past the escape value. If we increase the escape value and de-emphasize the boundary, we can see that the complement of the set is a dust:

Julia Sets for Powers of z <=2
I love these. If you're looking for a design for psychedelic wallpaper or a new tattoo, choose your exponent and then play with the Julia constant:



Mandelbrot and Julia Sets for Intermediate Powers of z
There's nothing to stop you entering a decimal number for the exponent either. Here's what you get:

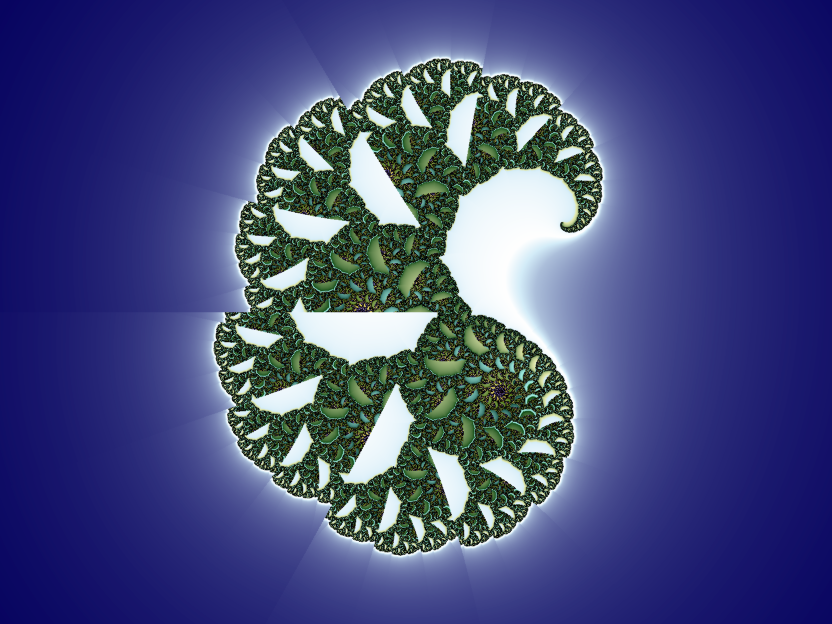
There is an obvious shearing effect; with the Julia set images the effect is more or less pronounced according to the magnitude of the imaginary component of c. Here's what's happening: raising a number to the 1.5th power is the same as cubing it then taking the square root. There are two square roots, but the generation algorithm only uses the principal square root. This is what causes the shearing: we are losing information. Given that this happens on every iteration, it is not computationally feasible to take both square roots into account because the algorithm would run in exponential time rather than linear time - we could maybe manage 20 iterations but 1000 iterations would take beyond the heat death of the universe to colour a single pixel!
Glynn Fractals
The Julia sets for 1 < P < 2 and values of c located close to the western boundary of the Mandelbrot sets have a characteristic form and are known as Glynn fractals:


A zoom into one of the bulb structures makes the tree structure of the above fractal apparent:
