Rational Maps
This formula makes Julia sets from the following class of functions:
zk+1 = zkP + c - λzk-Q
P is >= 2 while Q is <= -1. The + c is optional and allows us to perturb familiar Julia sets in interesting ways. Simply varying λ, P and Q allows us to produce a bewildering variety of forms. Credit is due to Robert Devaney for introducing me to the formula.
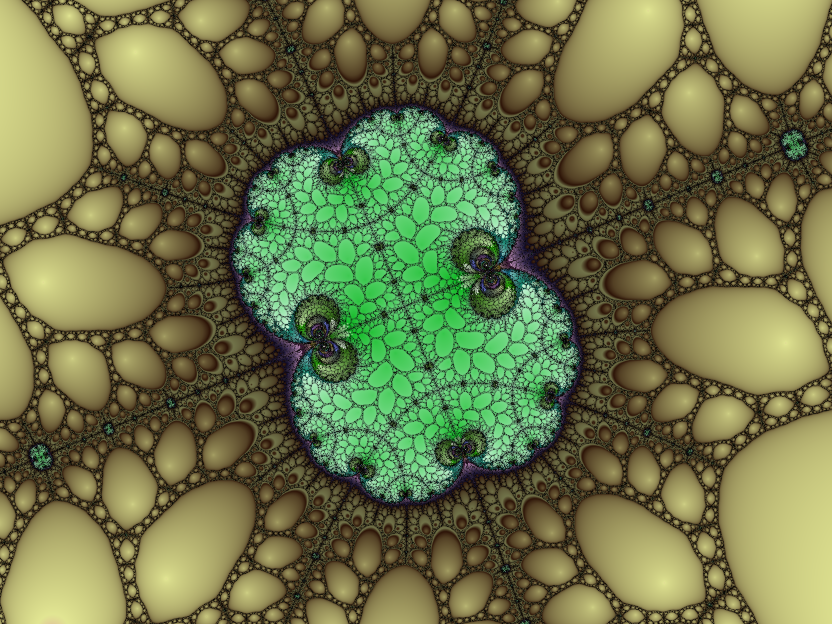
Despite the superficial resemblance to the standard Julia set formulas for zP (and if λ is 0, it is the same formula), the results are very different. If you load up the Rational map formula with all defaults, this is what you'll see:

The most obvious feature is that it's full of holes! The fractal is homemorphic to (topologically the same as) the Sierpinski carpet:

With Q = -1, it is possible to produce a homeomorph of the Sierpinski gasket:

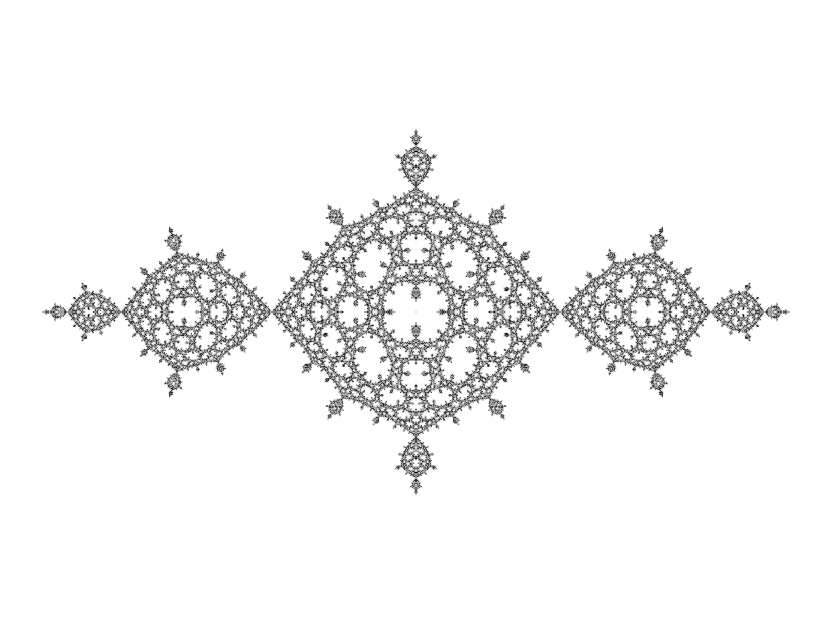
So long as c = 0, the order of symmetry is P + |Q|. This combination of parameters shows perfect four-fold symmetry:

Topology of the Rational Map Fractals
The zP + c Julia sets have essentially two forms: a Cantor set (an infinity of scattered points) or a connected set (topologically equivalent to a closed circle). If 0 escapes to ∞ under iteration, J(f) is a Cantor set. When P and |Q| are both > 2, the sets formed by the rational map formula can take three forms:
When z is large, the reciprocal term becomes insignificant and all iterations tend to ∞. The basin of attraction of infinity is denoted by Bλ. Because of the reciprocal term, 0 maps to ∞ after a single iteration. If the basin of attraction around 0 is enclosed by J(f) we denote it by Tλ since it is the trapdoor through which points inside J(f) escape. In addition, there are P + |Q| additional critical points which are solutions of fʹ(λ) = 0. Because of the symmetry of the function, we only need to consider one of these which we denote by νλ.
Cantor Set

Here νλ lies inside Bλ.
Cantor Circles
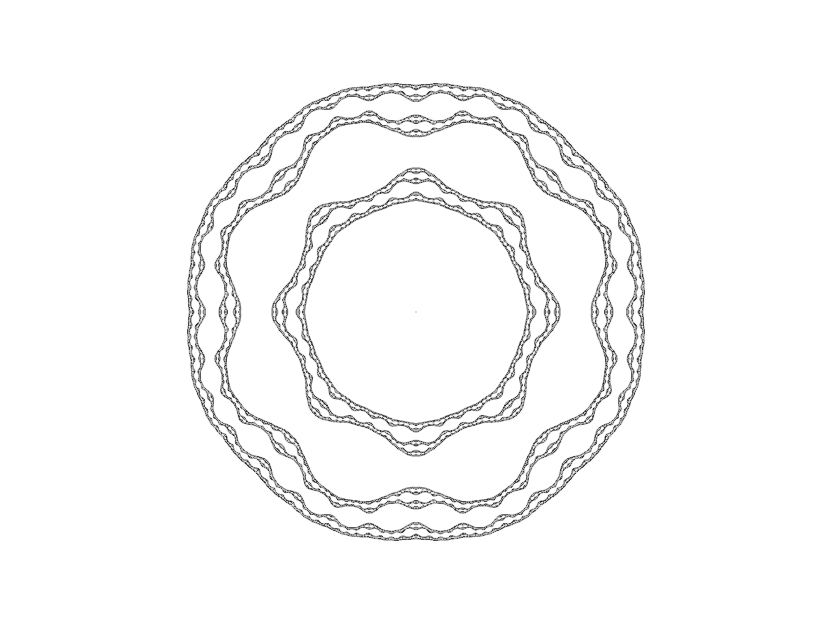
When νλ lies inside Tλ, J(f) takes the form of concentric, disjoint, simple closed curves.
Sierpinski Curve
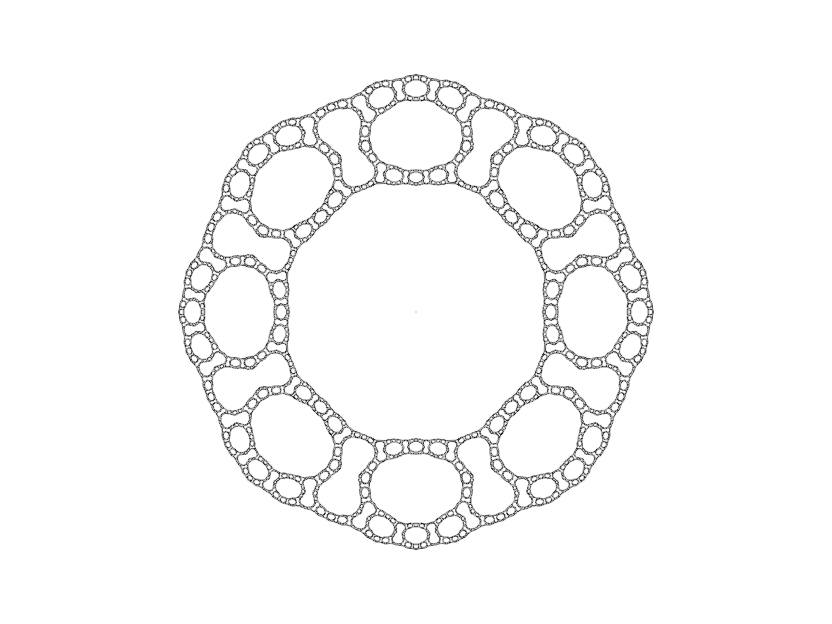
Otherwise J(f) is connected. If νλ ends up in Tλ under iteration, the form taken is a Sierpinski curve.
Colouring the Sets
Because the structures are delicate, the default settings de-emphasize the boundary. However, when points in J(f) are closely packed, showing only the boundary greatly improves the appearance, for example:
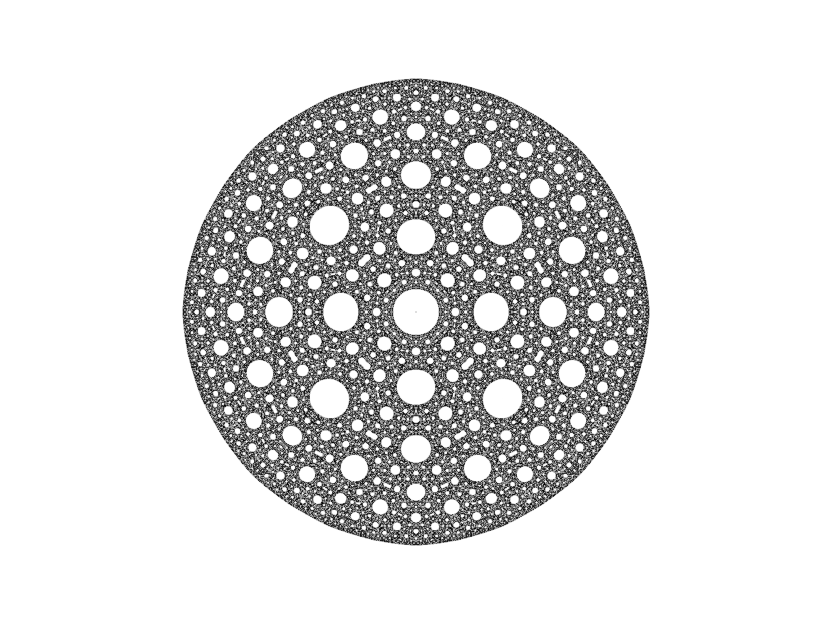
Exterior colouring for this one looks distinctly messy.
+ c: Perturbing Julia Sets
With c ≠ 0, we are able to put an entirely new spin on familiar forms:
Exploring Further
Unlike, say, the Phoenix formula which is hard to get anything out of, finding cool forms with this formula is as easy as falling off a log. Pretty much any combination of parameters will get you in the ballpark of something interesting and/or attractive. You've got four parameters to play with. Go wild!