What is a fractal?

It's easiest to answer this question with an example. Look at the following sequence of images:

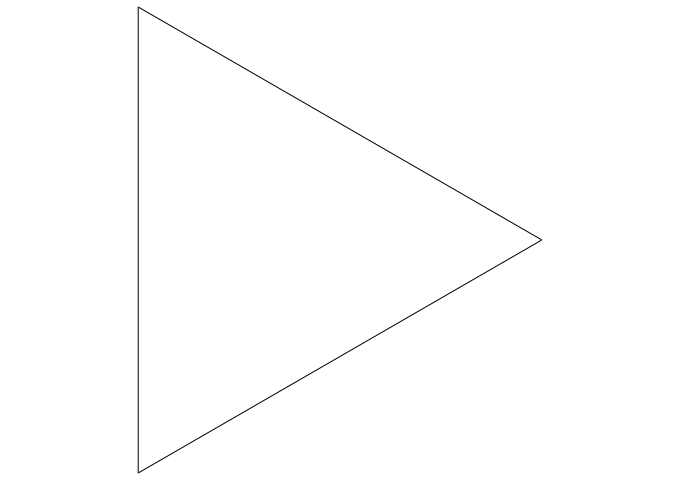
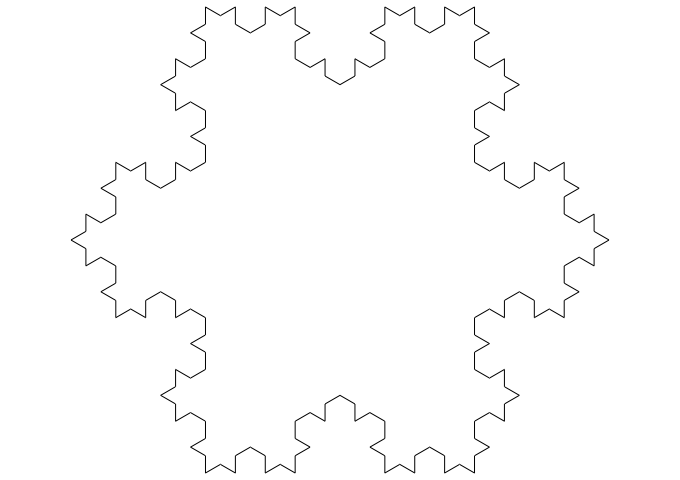
The Koch Snowflake after 0, 1, 2, 3 and 6 iterations

The sequence shows the evolution of a fractal called the Koch Snowflake after a number of iterations. The fractal is formed thus:

Start with an equilateral triangle
Remove the middle third of each side and replace with two sides of a smaller equilateral triangle
Repeat ad infinitum.

Despite its simplicity, the Koch Snowflake shows the essential characteristics that define a fractal:

Infinite, non-trivial detail
Self-similarity
Nowhere differentiable.

The term "fractal" was coined by Benoit Mandelbrot in a 1975 book Fractals: Form, Chance and Dimension

Infinite, Non-trivial Detail

In a trivial sense, a straight line has infinite detail: you can remove the tiniest segment and you get a straight line. But note the word "trivial". No matter how tiny a section of the Koch Snowflake you remove, you never end up with a straight line; instead you end up with something that still has infinite detail.

Self-similarity

The tiniest section of a Koch Snowflake scaled up is indistinguishable from a larger section. We can say that the curve displays exact self-similarity. Exact self-similarity is not a requirement for a fractal. The Mandelbrot Set, for example, shows quasi self-similarity where repeats of the basic form are found at all scales. Naturally occurring fractals show statistical self-similarity where the essential characteristics of the form are preserved at all scales. An obvious example is clouds: they look "cloudlike" no matter where you view them from: the ground, the top of a mountain or from above in an aeroplane.

Nowhere Differentiable

This requires a bit more explanation. For the moment, it is sufficient to know that the differential of a function gives you the instantaneous rate of change of the function. It works on the principle that no matter how sharply curved a function is, if you get in close enough, the graph of the function will appear to be a straight line whose slope you can measure. But remember that with the Koch snowflake, you never find a straight line, no matter how close you get in.

Non-integer Dimension

A curious property of the Koch Snowflake is that at every iteration, we remove one third of its perimeter but add two thirds back in. This means that that the length of the perimeter increases by one third every iteration. This increase in length is unbounded so that the length of the perimeter (and, indeed, the tiniest section of the perimeter) is infinite. Yet the area is clearly finite since one can draw a box of finite area that entirely encloses it. Now imagine that you remove a 3cm long section from the side of the Snowflake. If you only had a ruler that was 3cm long, you would measure the length of this section to be 3cm. But if you had a 1cm ruler, you could make four measurements and find the length to be 4cm. There is a formula that relates dimension to the number of units measured at different scales:

N ∝ ϵ^-D

N is the number measured, ϵ is the scaling factor and D is the dimension. For a 3cm long straight line, we measure 3cm when we use a 1cm ruler, so the above equation gives us:

3 = ⅓^-D

From which we can readily see that D = 1, since ⅓^-1 = 3. So a straight line has 1 dimension. No surprise there. However, a section of the Koch Snowflake gives us a measurement of 4 when we use a ruler one third the scale. Plugging these values into the formula gives:

4 = ⅓^-D

Rearranging the values gives:

D = -log_⅓4

⅓ isn't a particularly useful base for logarithms, so we can rearrange some more to get the values in terms of natural logarithms that we can readily compute:

D = -log 4 / log ⅓
  = -1.3862943611198906 / -1.0986122886681098
  ≈ 1.26186

So it seems that a section of the Koch Snowflake has a dimension > 1. The fact that we had an infinitely long perimeter enclosing a finite area suggested that the familiar rules of geometry no longer applied. The non-integer dimension is another way of saying that the dimension of a fractal is higher than the space it is embedded in.

Other Fractals

While the Koch Snowflake is useful for illustrating and analyzing the essential properties of fractal forms, it isn't very interesting in and of itself. Zoom into the Snowflake and you'll just see the same old wiggly line until you get bored, which won't take very long. Most fractal applications (this one included) focus on the endlessly fascinating forms produced by complex mapping functions, like this:

A Julia set from the Burning ship fractal

Yes, there's a reason why no-one ever made a poster or T-shirt of the Koch Snowflake!

Back to the index