Julia Sets and The Mandelbrot Set

Julia Sets

Take any mathematical function f(z) where z is a complex number (if you don't know what a complex number is, check out the five minute guide to complex numbers). The Julia set of f, denoted by J(f) is the set of numbers such that the tiniest change will radically change the value under iteration of the function. The counterpart to the Julia set, the Fatou set, denoted by F(f), is the set of numbers such that nearby values behave similarly under iteration. When applied to members of the Julia set, the behaviour of f is chaotic in the strict mathematical sense of tiny changes to initial values leading to large changes over time (or under iteration).

Examples of Julia sets

Consider an extremely simple, non-trivial function:

z → z2

J(f) is the unit circle (a circle of radius 1, centered on zero):

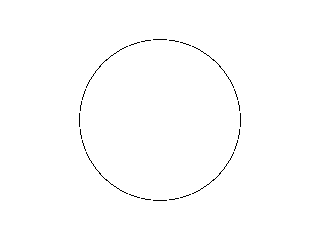
Explanation: no matter how many times you square 1, it's going to stay 1, because 1×1 is 1. However, make it just a tiny bit smaller, like 0.99999, and repeatedly squaring it will eventually make it converge on 0. Make it the tiniest bit bigger, like 1.00001, and repeatedly squaring it will eventually make it grow towards infinity. For the purposes of illustration, the Julia set is over-emphasized. It is, as should be apparent if you consider that the magnitude of a number in the set has to be exactly 1, infinitely thin (despite having infinitely many members). Speaking mathematically, we would say that the Julia set is uncountable and nowhere dense.

Now consider the function:

z → z2-2

J(f) is the line segment between -2 and 2 (Julia set is extremely over-emphasized):

You can do the mental arithmetic: -2 → 2 → 2...; 0 → -2 → 2...; 1 → -1 → -1... Any value outside this line segment will head off to infinity since if you square any imaginary number and subtract 2 the result is <-2; square this, subtract 2 and the value is now somewhat >2. Repeat and the value grows without bound.

Most Julia sets are nowhere near as simple:

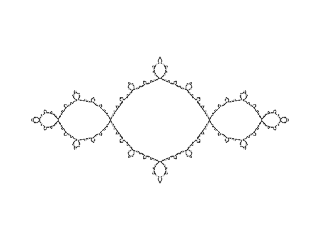
Evolution of Julia Sets

Why is J(z²-1) a fractal and J(z²-2) a straight line? It's easier to understand if we imagine the inverse iteration: start with a circle of radius 2 and then repeatedly apply the iteration function:

z → √(z - c)

The previous images have only shown the Julia set. The following illustrations use exterior colouring, since we won't have enough information to trace the boundary. We'll start with c = -2:

Each iteration, we shift all points of the circle left by 2 (which discards half of the points). We then take the square root which has three effects: values whose magnitude is > 1 contract, values whose magnitude is < 1 expand and the square root creates a mirror image since each number has two square roots. The result is two teardrops that are pinched at the origin. Repeat and you double the pinched teardrops each iteration while making them smaller. At infinity, the repeated pinching has made the tear drops infinitesimally small, leaving a straight line segment. Compare with c = -1:

There's still pinching going on, but the smaller shift means that the deviation from a circle is less dramatic which prevents the detail from being smoothed out. J(z²-2) might be considered a degenerate fractal: infinite detail but each element infinitesimally small.

Connected and Unconnected Sets

Take a look at the following image:

Notice that the Julia set doesn't quite join up. In fact, due to the fractal nature, it doesn't join up anywhere as this 20000x zoom shows:

This Julia set is unconnected. Now compare it to this:

Despite the intricacy, this set is a continuous line:

The second set is connected which means that, in theory, you could take a circle and pull and squeeze it into the shape of the Julia set without cutting it. A change of 0.0001i is the difference between a Julia set that is unconnected and one that is connected. What gives?

The Mandelbrot Set

The general form of the Julia set functions that we've been looking at is:

z → z2 + c

where c is a complex number of our choosing. What happens if we iterate over all values of c?

0 → c → c2 + c → (c2 + c)2 + c → ... 

One formal definition of the Julia set of f is that if f is an entire function (yep, Wiki link!), J(f) is the boundary of points that diverge to infinity under f. Therefore, values of c that head off to infinity are not part of this new set, but values which remain bounded are. When plotted, this set has a familiar form:

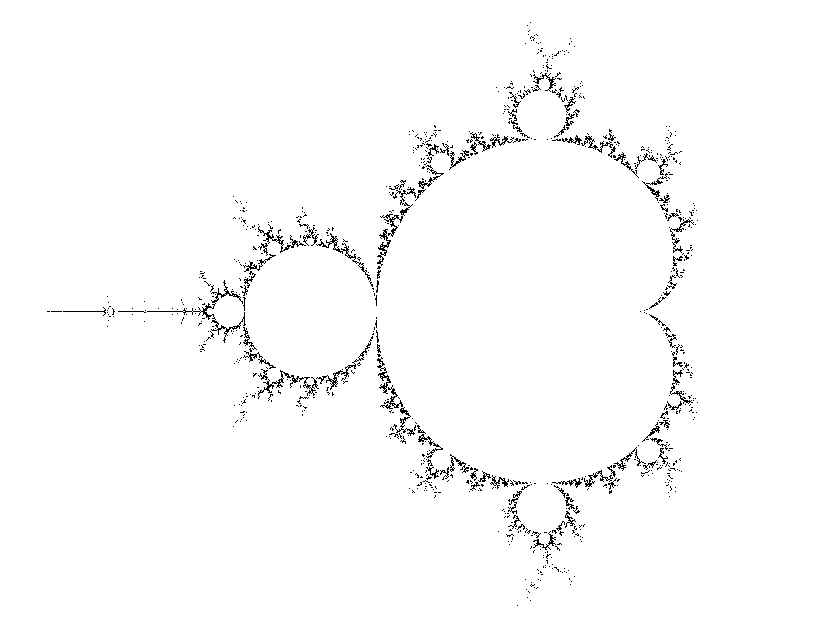
There is a reason that the iteration starts at 0. The derivative of z² + c is 2z. This derivative is 0 when z = 0, making 0 a critical point of the function. This means that members, c, of the Mandelbrot set are values for which the critical orbit (the iteration values starting at 0) remains bounded. If we were to plot the Mandelbrot set of the function z² - z + c, iteration would start at 1/2 since the derivative of that function is 2z - 1 which is 0 when z = 1/2, making 1/2 the critical point.

This is a different beast to the Julia sets. It is compact: along the real axis, it extends from -2 (the tip of the spike) to 0.25 (the cusp of the main cardioid). Along the imaginary axis it extends from approximately 1.227i to -1.227i. It is dense: points inside the boundary are members of the set. Its structure also shows a lot more variety than any Julia set:

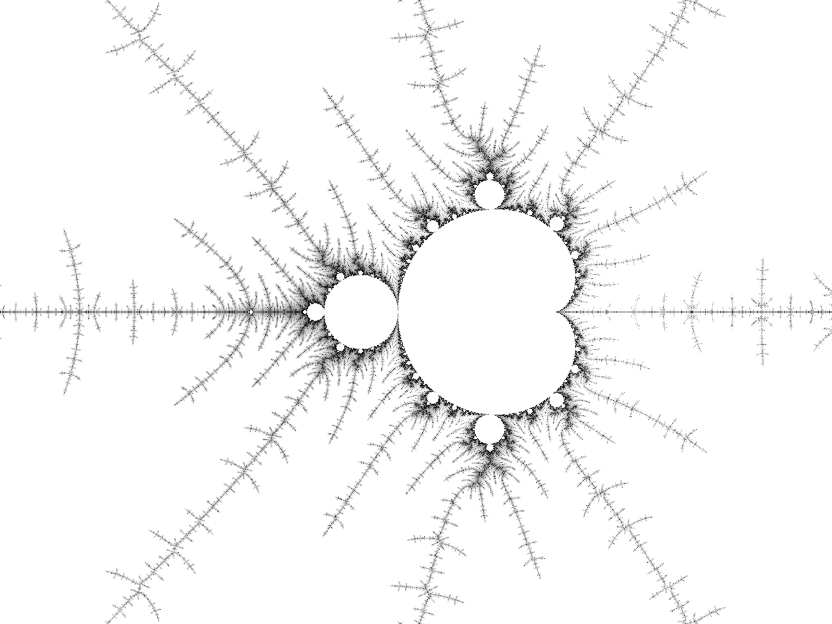
So what's the connection between the Mandelbrot set and Julia sets? The Mandelbrot set is the set of c such that J(z² + c) is connected since a Julia set is connected when the critical orbit is bounded. This means that we can use the Mandelbrot set as a directory of Julia sets: a point inside the set will give us a blob, a point some distance away from the set will give us a boring dust while points close to the border will give us Julia sets that are likely to be visually interesting. The Julia set for a point c resembles the Mandelbrot set in the region of c. To illustrate:

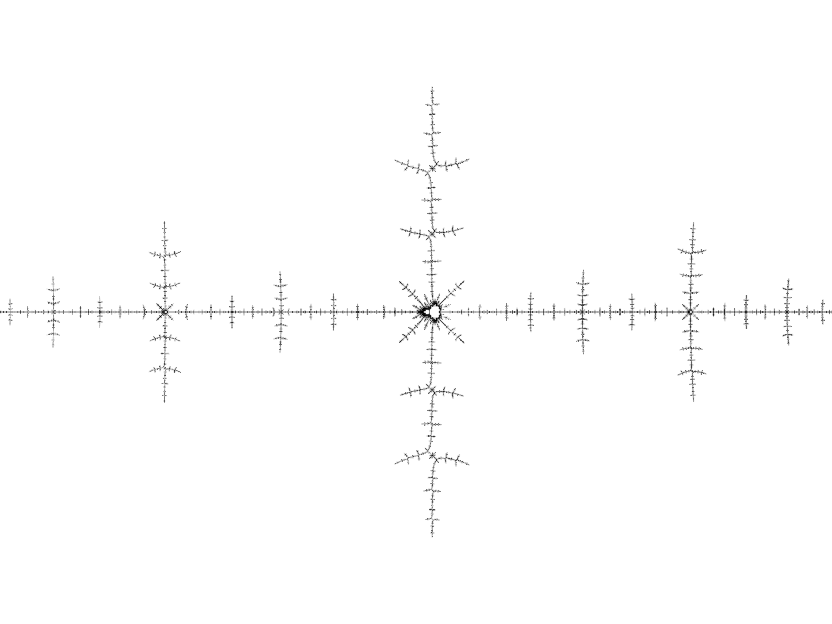
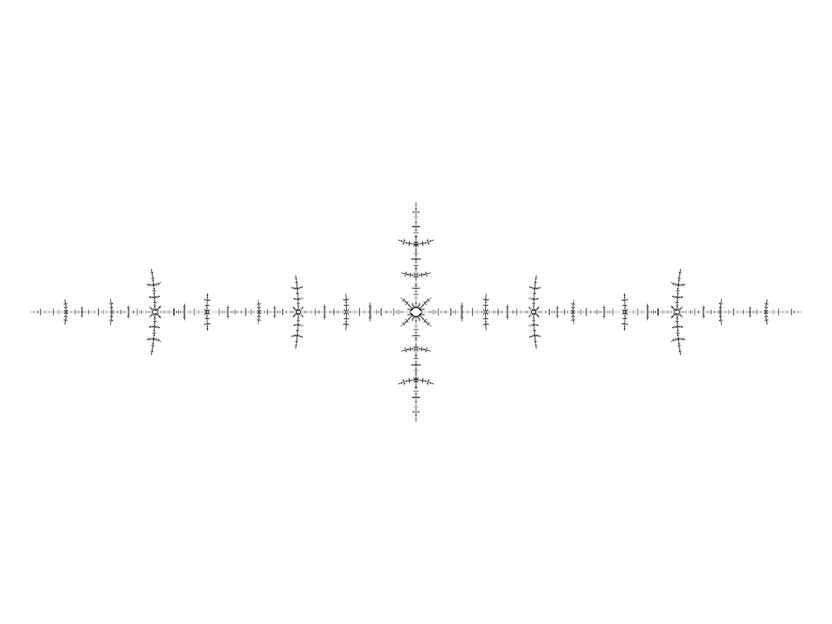
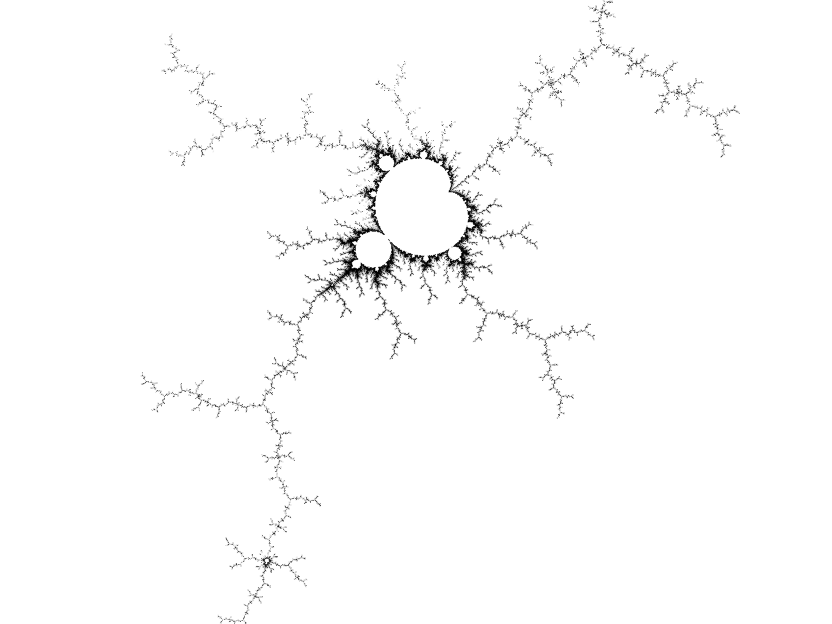
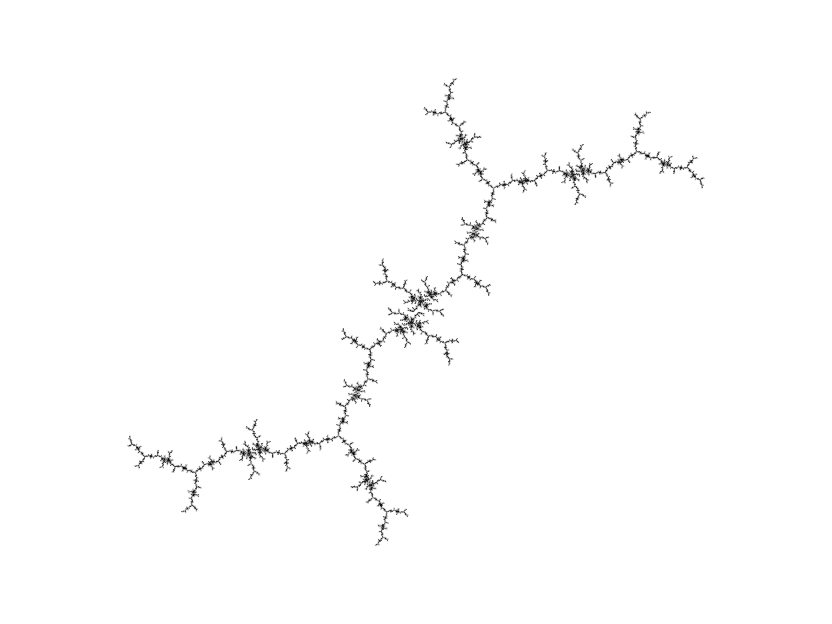
And the answer to the "What gives?" question earlier? 0.26 + 0.0016i lies just inside the Mandelbrot set, while 0.26 + 0.0015i lies just outside.

Mandelbrot- and Julia-style Iteration

The Julia sets and Mandelbrot set discussed in this article both use the same iteration function:

z → z2 + c

The difference between them is the nature of z₀ and c where z₀ is the first value in the sequence and c is the value added to z² as we apply the iteration. For the Julia sets, we have:

z0 = z; c = CONSTANT

For the Mandelbrot set we have:

z0 = 0; c = z

In both cases, z is the point in the complex plane under consideration. This leads to the observation that we can obtain different fractal images from the same iteration function by using either the initial conditions of a Julia set or the initial conditions of the Mandelbrot set. For convenience, I call the first a Julia-style iteration and the second a Mandelbrot-style iteration. This may not be entirely valid from a mathematical viewpoint, since Julia sets and Mandelbrot sets have very formal definitions, but it is a useful abstraction from a programming viewpoint.

All fractal images produced by this application use either a Mandelbrot-style iteration or a Julia-style iteration, possibly with minor variations (for example, the Nova fractal is obtained by a Mandelbrot-style iteration, but with z₀ = CONSTANT).

Back to the index