Newtonian Fractals

New Terminology

To understand Newtonian fractals, we'll have to get our heads around some new terms. A critical point of f is a value z such that f'(z) is 0. If the degree of the function is >= 2, ∞ is also a critical point (see the quadratic Julia sets where the critical points are 0 and ∞). A Fatou domain, F_i (where i is 1, 2, 3...) is an open set that contains at least one critical point of f and which is invariant under f meaning that the endpoint of a sequence of iterations of f of a point in F_i lies in F_i. The union of the Fatou domains F_i is the Fatou set, F(f). The complement of the Fatou set is the Julia set, J(f). J(f) is also invariant under f - iteration of a point in J(f) terminates in J(f). J(f) is repelling; this means that if we take a point w that lies close to a point z in J(f), the following condition holds:

|f(z) - f(w)| > |z - w|

The Julia set is the boundary for every Fatou domain.

The cycles in F_i are either attracting (sequence terminates in a finite cycle or a fixed point) or, rarely, neutral (the iteration sequence is annular). The type of attractor depends on the value of f'(z) at the attracting point A:

• If f'(A) = 0, z is super-attracting. If the second to kth differential is also 0, it is super-attracting with order k
• Otherwise it is attracting.

To illustrate these let's look again at the result of applying Newton's method to z² - 1 = 0:

• The two bright spots at ±1 are both the critical points and the attracting fixed points of the function. Since they are unique solutions of f, N'(z) = 0 at the roots and they are super-attracting
• The purple and blue areas are the Fatou domains, F₁ and F₂
• All iteration sequences in F_i terminate at the critical points (for this particular function at least)
• The imaginary axis (overemphasized) is the Julia set
• The Fatou domains are bounded by the Julia set.

If the equation being solved does not have d unique solutions, where d is the order of the equation, one or more of the roots will have a multiplicity m > 1. In this case, N'(A) = (m - 1) / m and hence is merely attracting rather than super-attracting. For example, z³ - z² - z + 1 = 0 has two roots at ±1. -1 is a unique root and super-attracting. +1 is a root with a multiplicity of 2:

Newton's Method Applied to Cubic Equations

If you select "Newtonian fractal" and use the default parameters, this is what you will see:

In case you're wondering, yes, the palette was very much tuned to create the diamond necklace effect! Although the standard view is pretty, the basin of attraction colouring option is more illustrative of what is going on:

The cube roots of 1, located at +1 and (-1±√3) / 2 are once again shown by the bright spots in the basins of attraction, but looking at the structure of the basins, it's no wonder that the best mathematical minds of the nineteenth century were unable to figure out what was going on. The boundary of the basins of attraction, J((2z³ + 1) / 3z²), does not trisect the plane neatly. It is fractal and cannot be other than fractal. Remember that the Julia set is the boundary of every Fatou domain. More precisely, every point in the Julia set is a boundary point of every Fatou domain so that if you drew an infinitesimally small circle around a point in J, it would contain points belonging to three different domains. This is impossible with normal geometry (try it: colour in a piece of paper with three colours in such a way so that everywhere two colours meet, the third meets as well; hint: you can't, not unless you generate a cubic Newtonian fractal). If you're surprised that there are three cube roots of unity, remember that raising to a power in the complex plane involves a multiplication of the angle (×3 in the cubic case). This means that any three numbers with the same magnitude that are separated by 120° will end up at the same point on the circle when cubed.

The fine links of the Julia set are shown very effectively with a change of palette:

Unlike the other Julia sets that we've looked at which lie inside a circle of radius 2, the Newtonian fractals extend over the entire complex plane and infinity is a member of J. Not only do points in J not converge but many diverge to infinity under iteration. Speaking mathematically, we would say that the preimages of ∞ are dense in J. The properties of the Julia set itself do not affect the effectiveness of Newton's method. Not only is the chance of starting at a point in J when making an initial guess close to 0, but any numeric errors (such as those due to finite precision in floating point calculations) will move the iterated value away from J.

Higher Order Equations

Using Newton's method to find the fourth roots of unity shows the geometric characteristics of the fractals generated by functions of the form kz^P + c:

We have P chains, dividing the plane into equal parts. Each chain is made up of P - 1 braids and the chains repeatedly converge on singularities. Basin colouring makes the chaotic behaviour of values close to J evident:

We can see that most values close to J do not converge on the closest root. Tiny changes to the initial start value will make a value converge onto any of the four roots. This chaotic behaviour means that Cayley's problem of predicting which of the P roots a given value will converge to is insoluble for P >= 3.

Pictures of the nth roots of unity are very educational and all that, but get a little bit samey. While playing with the polynomial terms can result in a lot of duds, you can also get some fantastic forms. Zoomed in, this is a good 'un:

Playing With the Relaxation Parameter

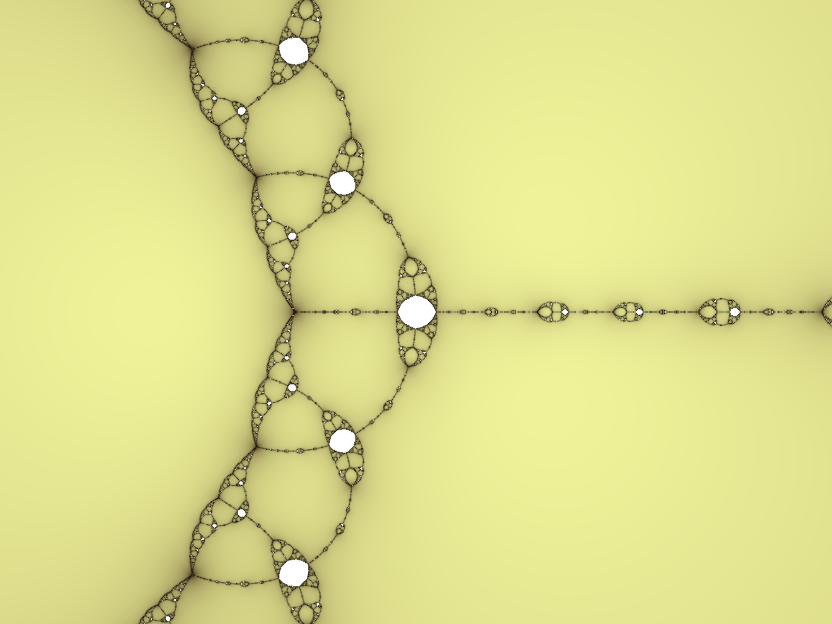
The above image is the Newtonian fractal for z³ - 2z + 2 = 0. The white ovals are areas where values do not converge to any root. The tangents of the function change direction at points close to each other in various places in the complex plane and if the initial guess is in one of these areas, the iteration will terminate in a periodic sequence of repeating values rather than a root of the function. We can make the function convergent everywhere with a little bit of under- or over-relaxation:

Values of R very close to 1 can create some interesting patterns:

The white area in the top image is a distorted version of the Basilica Fractal, the filled Julia set for z² - 1.

Values of R that differ from 1 by around 0.8 perturb the method to a degree that it no longer converges. Since convergence is the bailout condition for iteration, this will make generation quite slow because Newton's method involves a lot of arithmetic. Nonetheless, we can still end up with appealing results. For example, we can make a fractal from a quadratic equation:

Extreme values of R result in values that aren't mathematically meaningful; if the difference between two iteration values evaluates to NaN (not-a-number), iteration stops and whatever colour has been calculated up to that point is used. NaNs appear in the iteration function when the numerator and denominator are both infinity. This can still result in happy accidents:

Nova Fractals

The Nova fractal applies Newton's method and adds the pixel value on each iteration:

              f(zk)
zk+1 = zk - R·------ + c
             fʹ(zk)          

It gives us an additional parameter to play with, the value of z₀ which may be either an arbitrary complex number or the pixel value, signified by "c". Iteration stops when the difference between two iteration values falls below a certain threshold. The images produced tend to resemble shoot-em-up bosses. If you select Nova fractal with the default parameters, you will see this image (slightly zoomed for illustration):

One obvious feature of this formula is that a whole bunch of it seems to be missing: the curved rear encloses a void. The other Mandelbrot sets that we've examined all have critical points at 0 and ∞ which means that we only need to consider 0 since the basin of attraction of ∞ is outside the set by definition. In the general case when plotting the Mandelbrot set of a function we need to iterate from two critical points and test each for bailout condition. However, we are considering at most one critical point (and even that depends on the value of z₀). The result is that our image is broken in a number of ways.

When the input function to N(z) is of the form zⁿ - 1, you will find Mandelbrot islands when you zoom in, for example:

The colouring of these islands is deeply suspect: it depends on the iteration count. Although I can see that they're islands, I've not come up with a computationally tractable way of detecting that this is the case. Colouring areas that hit the maximum iteration count white or black or whatever does not work for this formula since the image is marred by blobs from other non-convergent areas. Therefore I rely on the exponential smoothing algorithm to give me a colour - any colour. For non-converging regions outside the islands I get the right one. For areas inside, I get something that is at least usable.

Modifying constant values in the polynomial terms, the value of R and the value of z₀ will result in the islands becoming distorted. Setting z₀ to 2 has an interesting effect:

If we set z₀ to c rather than a constant value, the sets produced are more compact and regular:

Playing with the relaxation parameter can produce some remarkable, slightly alien forms:

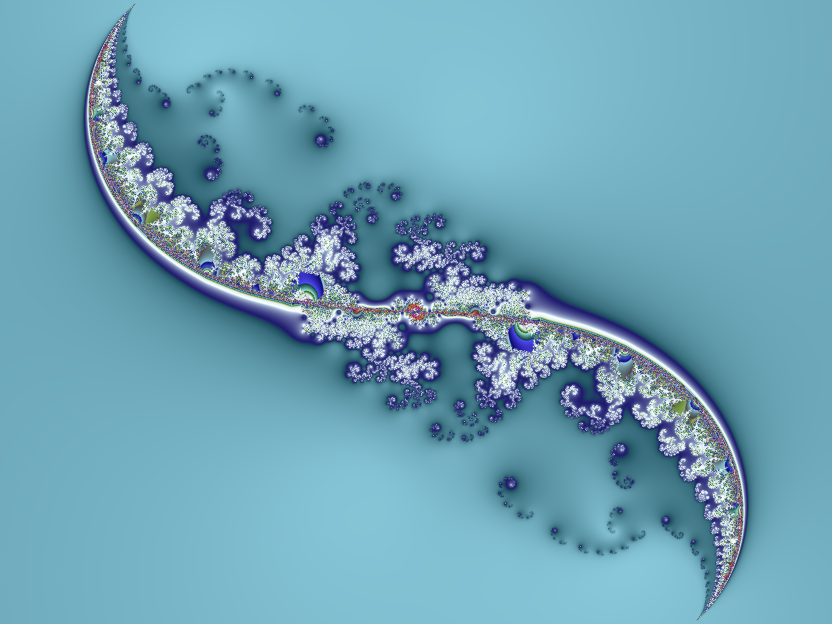
As with the Newtonian fractals, silly values of R can result in something kinda cool:

Although the f(z) + c style of the formula suggests that a Julia-style iteration is possible (it is), I've not included one because the results are extremely ugly.

Back to the index